School of Population Health
Appendix 2. Size of search
The program will evaluate, or estimate, the scale of the search for a particular p1,...,pq before it is begun and these values form #( Search), the target count during a search ( See 15.2 and See 18.1.1). The target count is based on exact and approximate formulæ for the number of partitions of size p1,...,pq, from an attribute set of m attributes, and on the scale of the sub-search required, if searching over floating cuts (See 14.4). The formulæ also provide the estimates of the search given in the Search Extent Box (see 18.1.1).
A2.1
Number of partitions of size p1,..., pq
Let Nq,m denote the number of normal disjunctive regular partitions of size p1,...,pq from an attribute set of m attributes (or, in the terminology of the lock and key algorithm in Appendix 1, Nq,m is the number of ways of selecting q groups of objects from a pool of m objects, with no embedding).
Consider first, the special case p1 = p2 = ... = pq = p. Then, with c = mCp, Nq,m = cCq since there are c possible groups and Nq,m ways of picking q of them.
When the pi's are not all equal then there is no simple general formula for Nq,m. Consider first q = 2 and suppose p1 ≥ p2. Let ci = mCpi for i = 1,2 and c12 = p1Cp2. Then it can be shown that
N2,m = (c1c2-c1c12)/e!
where e is the number of times a pi is repeated, that is, either 1 or 2. e = 2 when p1 = p2 and the formula coincides with that given by Nq,m above.
For the case q = 3 define, as above, cjk = pjCpk and, additionally, c'jk = m-pkCpj-pk, then it can be shown that
N3,m = (c1c2c3-c1c3c12-c1c2c13-c1c2c23+c1c12c13+c3c'13c'23)/e!
where e is the number of times a pi is repeated, either 1,2 or 3. The following table gives values of Nq,m by these formulae:
Table of Nq,m
| m | ||||
| p1,...,pq | 8 | 12 | 16 | |
|
||||
| 1 | 8 | 12 | 16 | |
| 2 | 28 | 66 | 120 | |
| 3 | 56 | 220 | 560 | |
| 1,1 | 28 | 66 | 120 | |
| 2,1 | 168 | 660 | 1680 | |
| 3,1 | 280 | 1980 | 7280 | |
| 2,2 | 378 | 2145 | 7140 | |
| 3,2 | 1400 | 13860 | 65520 | |
| 1,1,1 | 56 | 220 | 560 | |
| 2,1,1 | 440 | 2970 | 10840 | |
| 2,2,1 | 1680 | 17820 | 87360 | |
| 2,2,2 | 3276 | 45760 | 280840 | |
I have been unable to derive a general formula for q ≥ 4 when the pi's are possibly unequal. The best that I have achieved is an upper bound. Suppose the unique elements of p1,..., pq are denoted u1,...,ur where r ≤ q and that ui is repeated qi times. Then with di = mCqi and Mi = diCui
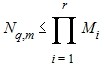
This upper bound may be pessimistic and may not give a good indication of the search size. However, in practice, searches with q ≥ 4 will be prohibitive anyway.
The actual number of partitions is 2 ×Nq,m if the disjunctive and conjunctive forms are both evaluated. The above formulæ are those used to produce the #( Class) values in the Search Extent Box (see below) .
When Up to p_1..p_q is checked in the Extent dialog, all partitions up to the specified size are generated, as discussed in section 14.2. Some of these may automatically be skipped to avoid duplication. Also if Conjunctive and disjunctive is checked, the search is effectively doubled, as discussed in section 14.3. In this case the overall search sizes are in the following table:
|
|
m |
||||||
up to p1,...,pq |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
3 |
76 |
176 |
340 |
584 |
924 |
1376 |
1956 |
2280 |
2,1 |
186 |
568 |
910 |
1596 |
2562 |
3856 |
5526 |
7620 |
2,2 |
246 |
820 |
2080 |
4434 |
8386 |
14563 |
23580 |
36310 |
3,1 |
346 |
1128 |
2830 |
5996 |
11298 |
19536 |
31638 |
48660 |
3,2 |
886 |
4492 |
14080 36554 | - |
- |
- |
- |
|
3,3 |
1266 73772 28360 | - |
- |
- |
- |
- |
||
|
||||||||
A2.2 Sub-search extent
If the search entails sub-searching over cuts with full fine tuning (see 16.1) , and each variable in the attribute set has precisely l levels, then the scale of every sub-search is exactly S = lvwhere v = p1+p2+...+pq and the full extent of a search is Nq,m×S.
Sub-searches will differ in their extent if variables have an unequal number of cuts and the full extent of the search is the sum of the sub-search sizes of each of the Nq,m regular partitions. This is not known in advance of actually doing the search. However, an estimate of the full extent of a search can be obtained from Nq,m×E(S) where E(S) is the expected size of each sub-search and which is calculated from
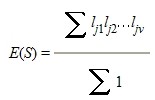
where li is the number of cuts for variable xi and the summation is over all ways of choosing vintegers, j1,...,jv, from 1,...,m, and ∑1 is the number of terms in the same summation. With limited fine tuning (see 16.1) Nq,m×E(S) provides an upper bounds which may be in excess of the actual search size. The formulæ for S or E(S) provide the #( SubSch) numbers in the Search Extent Box.
Search Extent Box
One feature of the output log that is given when a search is done is the Search Extent Box:
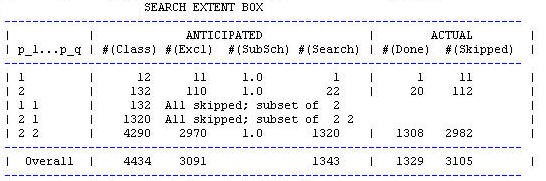
It gives a breakdown of the expected and actual extent of a search. The ANTICIPATED columns refer to numbers calculated before the search is carried out. The ACTUAL columns give the results of what actually occurred in the search.
The "#( Class)" column gives the computed anticipated extent of the p1,...,pq class, that is,Nq,m (see Appendix A2.1) . This number may be exact or an approximation. Approximations are tagged with a ~ symbol.
The "#( Excl)" column gives the number of partitions that are expected to be excluded, usually 0 but in iterative mode partitions not containing the attribute of the previous iteration will be skipped. (see Appendix 6).
The "#( SubSch)" gives the anticipated number of sub- searches required if cuts are floating. This value is 1 for fixed cuts. For floating cuts the number is an estimate of the expected number of sub-searches for each partition. The number is exact if every variable in the attribute set has the same number of cuts (see Appendix A2.2)
The #( Search) gives the anticipated total size of the search and is calculated from :
#( Search) = { #( Class)- #( Excl)} * #( SubSch)
The #( Done) column gives the actual number of partitions generated and #( Skipped) the number skipped.
Skipped partitions
Partitions may be skipped for a number of reasons. Primarily, they are skipped in iterative mode if the partition does not include the attribute found on the previous iteration, for they must then have been covered on previous iterations. Sometimes an entire class may be skipped and shown with the message All skipped; subset of ... This will arise when searching up to a given p1,...,pq when an entire class is theoretically determined as a sub-class of some other. A full discussion of why partitions may be skipped is given in Appendix 6.




